정렬 - 퀵, 힙, 기수

퀵 정렬

 

2개로 비균등 분할 -> 각 부분 리스트 퀵 정렬 (재귀 호출) : 각 리스트에서 피벗 선택

왼쪽 - 피벗보다 작은 수/ 오른쪽 - 피벗보다 큰 수

s-->                                                  <--e 

s는 앞에서 e는 뒤에서부터 이동하며 피벗값과 비교, s가 더 크면 stop & e가 더 작으면 stop, 값 교환

분할 정복법 사용

평균적으로 가장 빠름

 

퀵 정렬

각 부분리스트에서 피벗 선택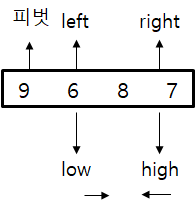

 void quick_sort(int list[], int left, int right) //퀵 정렬
 {  
   if(left<right){     
      int q=partition(list, left, right); //나누는 기준점
      quick_sort(list, left, q-1);   //재귀 호출
      quick_sort(list, q+1, right);  
    }
 } 
int partition(int list[], int left, int right)//나누기
 {
 	int pivot, temp;
 	int low,high;
 
 	low = left;                 
 	high = right+1;
 	pivot = list[left]; //각 리스트의 맨 앞을 피벗으로 잡음	
	do {	do
  			low++; //앞에서 이동하다가
		while(low<=right &&list[low]<pivot); //피벗값보다 크면 반복 stop
		do
  			high--; //뒤에서 이동하다가
		while(high>=left && list[high]>pivot);//피벗값보다 작으면 반복 stop
		if(low<high) SWAP(list[low], list[high], temp); //자리 바꾸기
	} while(low<high); //계속 반복
                
	SWAP(list[left], list[high], temp); 
	return high;
}

 

 

복잡도 : 대체로 O(n log n)

 

- 패스 수: log⁡ n / n (최선 / 최악 : 극도로 불균등하게 분할)

– 각 패스 안에서의 비교횟수: n /n

– 총 비교횟수: n ∗ log ⁡n /n^2

– 총 이동횟수: 비교횟수에 비하여 적으므로 무시 가능

 

---

 

힙 정렬

 

이진 힙 이용 

힙: 큰 수가 위로 오는 형태 (트리 구조)

힙

 

정렬 방법

- intial heap 구성

- 가장 상위의 수 제거

- 가장 끝 수를 상위에 넣고 다시 힙 재정렬 

 

#define  SWAP(x, y, t) ((t=x,x=y,y=t))
void adjust(int a[], int root, int n)//힙 재정렬
{
   int child, rootkey;
   int	temp;
   temp = a[root];
   rootkey = a[root];
   child = 2 * root;
   while (child <= n) {
      if ((child < n) && (a[child] < a[child + 1]))
         child++; //형제끼리 비교 -> 더 큰 놈을 child
      if (rootkey > a[child]) 
         break;
      else { //자식이 더 크면
         a[child / 2] = a[child]; //자리 바꾸기
         child *= 2;
      }
   }
   a[child / 2] = temp;
}
void heapsort(int a[], int n)//힙 정렬
{
   int i;
   int temp;
   for (i = n / 2; i > 0; i--) //5~1
      adjust(a, i, n); //5~10 /4~10/3~10...1~10 힙 구성
   for (i = n - 1; i > 0; i--) {//9~1
      SWAP(a[1], a[i + 1], temp); //맨 위를 맨 뒤랑 자리 바꾸기
      adjust(a, 1, i);//1~9/ 1~8...1 재정렬
   }
}

int main()
{
   int  list[] = { -1, 26, 5, 77, 1, 61, 11, 59, 15, 48, 19 }; //인덱스 0번은 의미없는 자리
   int	i;

   heapsort(list, 10);

   for (i = 1; i < 10; i++) //1부터 출력
      printf("%d ", list[i]);
}

 

복잡도 : O(n log n)

 

하나의 데이터가 힙을 찾아가는 시간 : log n

 

---

 

정렬 복잡도 비교

 

실행 시간